Making Math Visible
Super SOMA


SOMA is a cube-based geometric puzzle designed by Piet Hein in the 1930's. It is a well-known commercially available mechanical puzzle, typically a few inches in scale.  The goal is to assemble the pieces into a cube and other shapes.  SOMA is an excellent activity for developing spatial reasoning and abstract logical thinking. Students will immediately see connections to Tetris and Minecraft.

In this workshop, students will learn about this classic puzzle by constructing the individual pieces out of wood cubes and solving a progression of problems that lead up to a giant cardboard version of this versatile puzzle.  Students will be left with their own hand-size wood version for continued play and exploration.  The classroom will be left with the giant SOMA which can be displayed and used repeatedly.  This workshop provides a basis for a rich set of optional follow-on activities.  The physical objects will be enjoyed by students throughout the rest of the year. 

While there is significant content that older students will appreciate, elementary students do particularly well with SOMA and enjoy continually challenging each other with puzzles throughout the year.

The wooden and cardboard aspects are presented separately below.  We recommend doing them in succession, with the wood first, but either could be done independently or the two could be interleaved.

This activity provides rich classroom material for teachers following the Common Core Standards for Mathematical Practice.  This lesson also provides cross-curricular connections to art and architecture.


Detailed Instructions for Wood SOMA

Time Required:  1 Hour

Materials

Notes:
  1. In the end, only 27 cubes are needed per student, but for the discovery phase of this activity, it is important to have extras available.

  2. It works best if the cubes really are cubes.  Wood "cubes" can be found at Dollar Stores and other sources, but beware that some are not perfectly cubical and would affect the quality of the fit.

  3. Glue brushes work better with older students. Two methods are presented below for gluing, one with and one without brushes.


Part A.  Shape Discovery

 1. If you do have a SOMA set to show as an example, keep it hidden initially.

2. Place a supply of cubes on each table sufficient for each student to have at least 30 cubes.

3. Tell students they will be joining cubes together square-to-square to make larger modules which satisfy the following conditions:
 Ask students to build as many possible solutions as they can.  Give them time to explore and discuss with their neighbors.

4. Students will discover that seven acceptable modules can be made:


Ask questions to solicit the following observations: There is no module with just one or two cubes because that would be a rectangle. With three cubes, only one module is possible: a small "L" shape. The straight-line 3-cube possibility is ruled out because it is a rectangle. There are six possibilities with four cubes.  A square of four cubes is ruled out because that is a rectangle.  Two of the four-cube shapes are mirror images.  These two pieces should be discussed at length because some students will find them confusing.  It is helpful, especially with younger students, to have them position the two modules with a line of symmetry between them (e.g., a pencil) to emphasize the mirror relationship:


They are related by a mirror transformation, but can not be rotated to look like each other, so both must be included in the solution set.  At the end of this step, each student should have all seven modules built (not glued yet) even if they did not discover them all initially.

Part B.  Assembly

 5. Remove all the extra cubes from the desks.

6. There are two methods for gluing the cubes together:
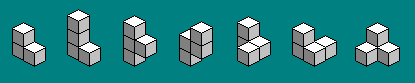
Brushing Method.  Using a small paint brush, apply a thin layer of glue to entirely cover each of the two faces that will be joined.  The thinner the layer of glue, the better, because it will dry faster and look neater.  This method works best with older students who are comfortable using a brush.
Dipping Method.  Squirt a small puddle of glue on to a scrap of cardboard or heavy paper. Dip one of the two faces to be joined into the glue. Rub it against the mating face and swirl them so both faces are entirely covered with glue. 
Have students make each module, incrementally adding one cube at a time.  Check carefully that cubes join together perfectly face-to-face.  Misaligned cubes would cause problems later when building larger constructions with these modules.  With younger students, teachers should check each piece and realign them if necessary before the glue dries.  Double check the two mirror-image pieces.  The modules should just sit on the desks, held together by gravity while the glue dries.

7. While the glue is drying challenge the students to think of a shape they could try to make with their seven modules. Ask younger students to first count how many cubes there are all together in the set of seven pieces. To make a brick-like three-dimensional array, the total, 27, would have to be expressed with three factors as either 1x1x27 or 1x3x9 or 3x3x3.  Looking at the pieces, students can visualize which of those are impossible to build.  To be perfectly clear about the logical arguments, you can solicit the idea that the 1x1x27 is impossible because none of the pieces are straight lines.  Furthermore, three of the pieces stick out of the plane no matter how they are oriented, so the flat 1x3x9 rectangle is also not possible.  This leaves the 3x3x3 cube as the only cuboid shape students can try to build.

8. If the glue is still drying, you can develop other questions such as:  What brick-like 3D arrays might be made by combining the sets of all students that are in the class?  How many students would have to be in the class if all the SOMAs were to be put together to make one giant cube?

9. Once the glue is dry, let students play with their pieces. It is worth giving students a significant amount of time to explore. When different students build the cube, ask them to determine if their solutions are the same.  Ask them to rebuild the cube in as many ways as they can.  At some point, you can tell them that there are 240 different solutions, not counting rotations and reflections.

10. You can show students some of the many additional shapes that can be built with SOMA.  Here are some of our favorites: the crystal, the tunnel, the dog, the dinosaur, and the skyscraper.  Optionally hand out the challenge sheet.  Many more challenges can be found online.
 

Possible Extensions

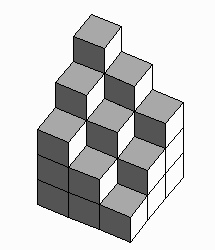
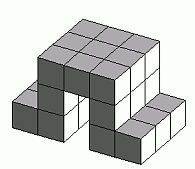
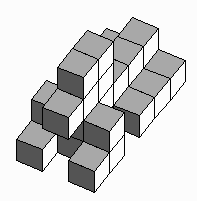
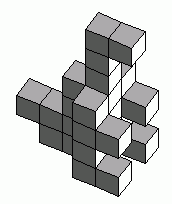
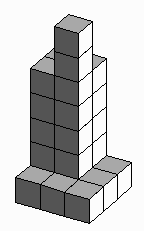
Student Design Challenge. Ask students to design their own shapes and challenge each other to recreate them.

Multiple Set Constructions. Students can combine two or more sets to create larger constructions.

Connection to Tetris and Minecraft. The rules above lead to these seven pieces, but students can explore other rules of their own choosing and see what shapes can be created following those rules.  For example Tetris allows all shapes, including rectangles, with exactly four cubes, but they must lie in a plane.

Other Materials.  Make a SOMA set in some other material, e.g., you can use 3D design software and make a set on a 3D printer.

Additional Analysis.  The possible 3x3x3 solutions can be analyzed with simple arguments.  For example, by considering which pieces can cover the eight corners of a cube, you can show that the "T" shaped piece must always be placed with its row of three cubes along an edge of the 3x3x3 cube, and there are no solutions with it along the middle of a side or through the center of the 3x3x3 cube.  See Winning Ways for your Mathematical Plays (Academic Press, 1982) by Elwyn R. Berlekamp, John H. Conway, and Richard K. Guy.

Free Time Activity. If the SOMA sets are kept in the classroom, young students can enjoy playing with them during periods of free time.


Detailed Instructions for Giant Cardboard SOMA

Time Required: 

Materials

Notes:
  1. One-foot cubes work well with elementary students, but you can use larger cubes with older students.  We have used 24-inch cubes with college students.
  2. It is much easier to apply the tape if you use a dispenser.

Steps

1. Show students how to build one box.  When closing each end of the box, apply tape not just across the center seam but also to the two sides.  Tell students never to sit on the boxes.

2. Ask students to work in groups to make the 26 remaining boxes.

3. Divide the class into seven groups.  Hand each group a wood SOMA piece which they will scale up to a large size.  The trickiest pieces to assemble are the two mirror-image ones.  Remind those groups to be extra careful.  Each group will take three or four boxes to make their piece.  Ensure when joining two boxes that the faces mate square-to-square without offset.  It is something of an engineering challenge to get the tape to hold well.  Group work is important.  Two students can hold boxes together while a third student runs tape along the joints.  Sometimes it helps to also run a band of tape all the way around the middle of two boxes, like gift-wrapping ribbon.  After applying the tape, a useful trick is to rub it with the back of the fingernails (or other hard object) to create a stronger bond between the tape and the cardboard.

 

4. After students walk around to check that all seven pieces are correct, it is time to build the giant cube.  All the students can help in putting it together. 

5. Through communication and teamwork, students can work on a series of large-scale SOMA challenges that they choose.

6. An excellent communication exercise is to ask a student to choose a model, make it with the small SOMA, and then give blind instructions to the group to replicate it on the large scale.  This will lead them to understand the value of clear communication, nomenclature, and geometric description.  Students will realize the importance of naming each piece and using precise language for describing intended rotations.


Possible Extensions

The Wood SOMA extensions listed above also work on this larger scale.

Big Thing each Day.  If you keep the giant SOMA in your classroom or have a public place in the school for displaying it, it is fun to have students change the shape regularly.  Daily or weekly a different group of students or staff might have a turn at choosing and building a new construction.  This is a great way to make math come to life in a visible way.

Decoration. Graffiti, paint, stickers, etc. can be applied imaginatively.