Making Math Visible

Rings and Strings
 

In this workshop, students make string figures within a circular ring.  Ideas of addition, subtraction, clock arithmetic, multiplication, sequences, and patterns can be developed while creating an attractive ornament to display.  We provide paper worksheets and templates for laser-cutting wood rings of various sizes.  For first or second grade students, a circular string pattern in a ring of twenty or thirty points is sufficiently complex.  Older students can assemble much larger rings and can create a cardioid after making circles.

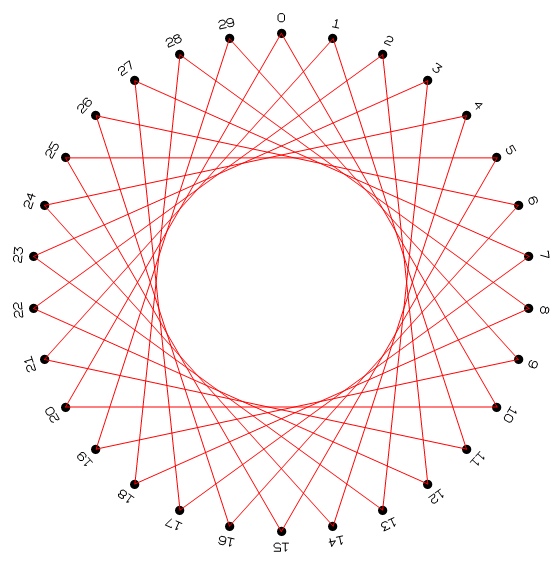
The basic pattern is to connect each hole with the hole k steps away.  This creates a circular opening centered in the ring, tangent to each string.  Doing this with one continuous string introduces a secondary problem of how to connect the visible segments using short segments on the back.  Then multiple patterns of different colors and with different values of k can be combined on one ring to create more interesting designs.  An optional extension is to move from addition to multiplication, by connecting each hole i with hole 2i, which creates a cardioid shape from the tangents.

String curves have a long history in mathematics education, going back to Mary Everest Boole, wife of the mathematician George Boole.  A classic 1906 book by Edith Somervell popularized the subject. Nowadays, the terms "curve stitching" or "string art" are used for variations of this activity; searching for them will produce many additional resources.

This activity provides rich classroom material for teachers following the Common Core Standards for Mathematical Practice.  This lesson also provides cross-curricular connections to art and architecture.


Detailed Instructions for String Rings


Time Required:  1 Hour

Materials

Notes:
  1. The ring templates can be scaled to be larger or smaller in diameter. Select the number of holes appropriate to your student's level. For elementary students, a 6-inch diameter, 30-hole ring is a good start.  For 6-inch diameter rings, 1/8 inch thickness plywood works well.  For 1-foot diameter rings, use 1/4 inch thickness.
  2. Larger rings can be assembled from arcs, as described below.
  3. We colored the rings shown here with a bright yellow water-based stain.
  4. The 30-hole ring, adding by 10 is the easiest way to begin.
  5. We found that the string aspects of this activity are difficult for many second grade students, even though they can do the "minds on" drawing part.
Part A.  Minds On

 1. Hand out a pencil, a ruler, and one copy of the 30-dot handout to each student.

2. Discuss the numbering of the dots. You can point out that mathematicians often like to start counting at zero.  It is a natural beginning.  The dots are numbered 0 to 29, so there are 30 dots.  Tell students that if they ever need larger numbers, to work as if the numbering keeps goes around, e.g., on a 30-dot sheet, after 27, 28, 29, you can act as if the next dots are 30, 31, 32 should you ever need those numbers (even though they are labeled 0, 1, 2). With older students you can discuss "clock arithmetic" or say to do everything modulo 30.

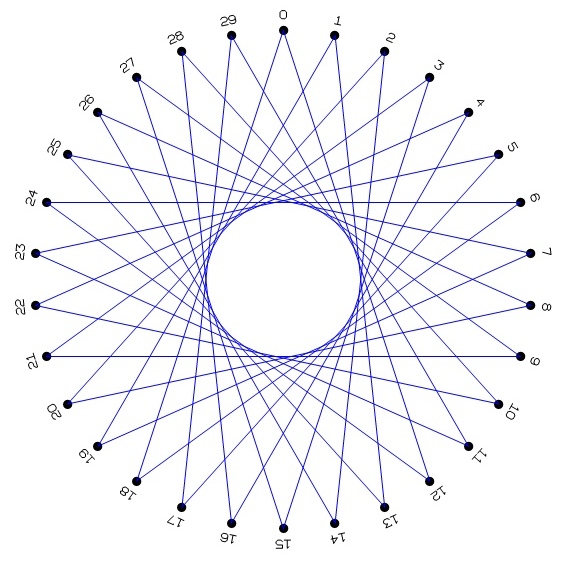
3. Ask students to use their straightedge to draw a line from dot 0 to dot 10.  And another line from 1 to 11.  And another from 2 to 12, and generally from each dot i to dot i +10. 

4. For the last ten lines, students will see how the numbers 0-9 are used again to represent 30-39, e.g., the line from 27 to 37 ends at the dot labeled 7.  The result should be like the pattern shown here in red.  Point out that "neatness counts" in the sense that the design will look better if the lines are straight and go directly from dot to dot.



5.  Ask students to choose a different number than 10 and similarly make 30 lines, each going from i to i + whatever number they chose.  Call their chosen number k; then each line goes from i to i+k, for all 30 possible values of i.  This can be done on a new sheet or on the same sheet but in a new color.  At this point, students can be given time to explore, compare their results, and try to understand the effect of their different choices for k.

   
6. Discuss the results and the effect of the different choices for k.  Students who chose a smaller number, i.e., k < 10,  will have a large opening, because the lines stay nearer the circumference.  If a student chose k=1, the result is just one big 30-gon and the lines never cross.  Values in the range 10 < k < 15 give a smaller central opening.  If a student chose k =15, the lines all cross at the center.  If a student chooses a number k that is larger than 15, the result is the same as if they chose 30-k, for example, choosing 29 gives the same diagram as choosing 1; or choosing 20 gives the same diagram as choosing 10. Discuss why. (Answer: Because of the "clock arithmetic," going forward 29 is the same as going backwards 1; going forward 28 is the same as going backwards 2, etc.).  What choice would give the smallest hole? (Answer: 14 or 16.)  For students familiar with negative numbers, you can discuss how 29 = -1, modulo 30, etc. and choosing k gives the same result as choosing -k because it gives the same set of lines when thought about from the other end, i.e., line that goes from i to i + 20, when thought about from the other end goes from (i + 20) to (i + 20) + 10).
 
Part B.  Hands On.  Rings and Strings



7. Hand out a laser-cut wood ring to each student.  [Note: these instructions assume you use a 30-hole ring; Adjust if you use the ring with 20 holes (for first grade students) or 50 holes (for older students).] Tell students that instead of using pencil and paper, we can stretch a string between two holes to make a line.  Give each student a skein of embroidery string (typically 8 to 10 yards).  Before starting, ask them to think about the difference between drawing lines and threading the string. How can the pattern be made with one continuous piece of string?

8. Students can each choose whether the side with numbers or the side without numbers will be the front. Every time the thread goes through a hole, it switches from front to back or from back to front.

9. Explain to students that they will run the thread through the holes of the ring to make a pattern, but that we want the pattern to be all on one side of the ring, so it can be fully seen, not partially hidden on the back.  Whatever side is front, we want the lines we "draw" in thread to be on the front, so we need to make short connecting hops on the back of the ring, analogous to when you lift up your pencil at the end of one line and move to the start of the next line.  Ask if there is a systematic way to do this.  Discuss ideas.  One thing to discuss is that it will look the same in the end no matter what order the strings are placed; you don't need to do the strings in the order 0, 1, 2, 3, ..., as long as each string segment is the same length and you eventually do all thirty of them. And another idea is that a sting from a to b looks just like a string from b to a, so it would be OK to go backwards if that ever helps.
 
Note: There are two natural ways we have found to run the strings continuously, using short hops on the back.  We call them the "Back and Forth" method and the "Skip Around" method.  The back-and-forth method is slightly more complex, but works the same way for any k.  The skip around method is more symmetric and more interesting to think about how and why it works, but you have to pick a good move for the back depending on the choice of k, so we recommend it for older students.

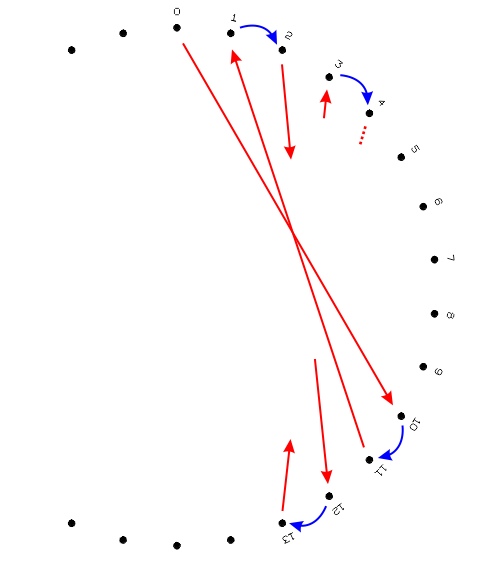
10. The Back and Forth Method.  The easiest way to make all the lines is to alternate going forward and backward, e.g., going forward from i to i + k when i is even and going backward from i + k down to i when i is odd.  (It is easier to do than to explain.)  For example, if k is 10, go from 0 to 10 on the front, then to 11 on the back, and from 11 down to 1 on the front.  Then go from 1 to 2 on the back and you are ready to go forward again.  In this way, the segments are made in order 0, 1, 2, 3, ..., but half of them are done "backwards" from the high number to the low number.


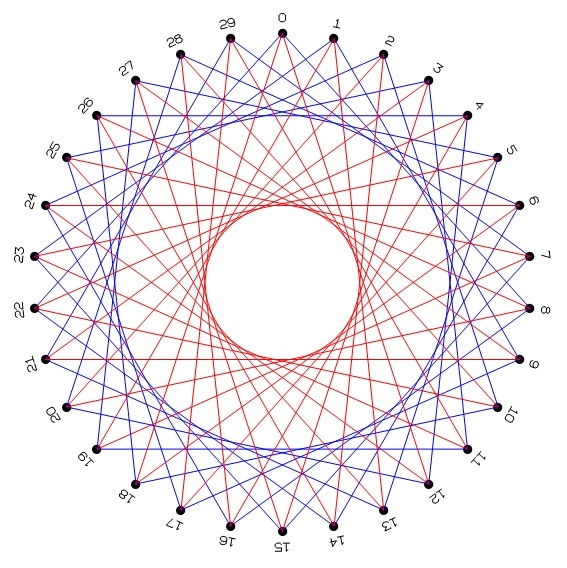
  11. Explain the method, perhaps drawing a diagram on the board like the image above.  In this diagram, the red represents the segments on the front that we want to "draw" with the thread.  The blue represents short hops on the back to move us to the next segment.



12.  Ask students to open the embroidery thread, being careful not to tangle it.  Wrap the end around the 0 hole and tie a knot to start the thread and prevent it from getting loose.  Leave a bit of the end hanging; it will be useful later, to tie off the end when complete.


13. Go from 0 to 10 on the front, to 11 on the back, from 11 down to 1 on the front, then to 2 on the back.  This is one back-and-forth sequence.  Keep the string fairly tight, so the lines stay straight and will not fall out of the holes.



14.  Continue with the back-and-forth moves.  You go forward k from the even numbers and you go back k to land on the odd numbers.  After each back-and-forth, you have completed two of the 30 desired lines and made two small connecting hops on the back.


15.  You should eventually end up back at 0 after making all 30 segments.  Check that everything is correct and tie off the end.  You can leave a hanging loop for displaying it.


16. When finished with all 30 segments, optionally add another set of 30 strings in a different color with a different choice of k.  The above example started with k = 10 in red, then added k = 8 in blue.


Young students may need help to focus on the algorithmic aspects of the string pattern even after they master the drawing.


A variation that some students find natural with the string is to go +10 on the front and -9 on the back.

 
Here are steps 10-16 again, using the Skip Around method.

 10. The Skip Around Method.  This is a much better mental exercise in addition.  Let k be the chosen "adder," so each line is to go from some i to i+k.  In this method we always move forward k on the front then make a small move on the back which is always the same.  For example, if k = 10 on a ring of size 30, go from i to i+10 on the front, then forward one more to i+11 on the back, then make make another forward +10 on the front, then move forward one more on the back, etc.  In this way, all 30 lines eventually get made, but in a different order. 



11. Ask students to open the embroidery thread, being careful not to tangle it.  Wrap the end around the 0 hole and tie a knot to start the thread and prevent it from getting loose.  Leave a bit of the end hanging; it will be useful later, to tie off the end when complete.


12. From 0, on the front go to k.  On the back go to k + 1.  Continue the pattern: on the front add k; on the back add 1.   Keep the string fairly tight, so the lines stay straight and will not fall out of the holes.
 

Continue in this way, always going +k on the front and +1 on the back.


13.  You should eventually end up back at 0 after making all 30 segments.  But if you made even one addition error along the way, then you will see it doesn't close up properly.  After checking for correctness, tie off the end.  You can leave a hanging loop for displaying it as above, when finished with all 30 segments.

14. Students may now add another set of 30 strings in a different color with a different choice of k. They should discover that the method works well for some choices of k, but fails for certain other choices of k.  This is an opportunity for them to analyze and mathematically model the situation.

15.  With older students, you can ask: What if k was 14 and you tried this?  It wouldn't work!  You would go from 0 to 14 on the front, then +1 to 15 on the back, then +14 to 29 on the front, then +1 on the back brings you to 0 again, and that hole is already complete.  One approach is that whenever you come to the front where you already have a string , just move forward an extra one on the back, to get to a new position that needs a string. This works fine, but a mathematical purist will be unhappy that the back isn't perfectly symmetrical. A different approach for k = 14 is to go -1 on the back each time (instead of +1 every time).  This works consistently for all 30 lines.  One can experiment and see that going -1 on the back would not work when k=10, though +1 on the back did work.   So for each k, there are choices for the back which do not work and choices which do work. Which work?  This is a good problem to pose to students familiar with prime numbers and factoring.  They may want to use the sheets with numbered dots to help understand the cases.



Example with 20-Hole Ring


For this example, you can go +8 on the front and -1 on the back.




The back has all the -1 steps.




Here, we have added a second layer, going +6 on the front and +1 on the back.

Part C.  Conclusion

With older students, you can discuss why the back-and-forth method always works and why the skip around method only works for certain choices of what to do on the back.  For some choices you end up back at 0 before all 30 lines have been drawn.  To understand what is happening, think about the net motion after moving k on the front and j on the back.  This brings you to a new hole on the front, where you repeat.  If k + j divides evenly into 30, then it ends too soon and you need to do something a little different on the back to continue.  If k + j is 7, 11, or 13, it works fine, e.g., 10+1 or 14-1.  In general, if k + j has any divisor greater than 1 in common with the number of holes, the process ends too soon.  So you can first choose k for its aesthetic effect then choose j to make k + j have the value you want. 


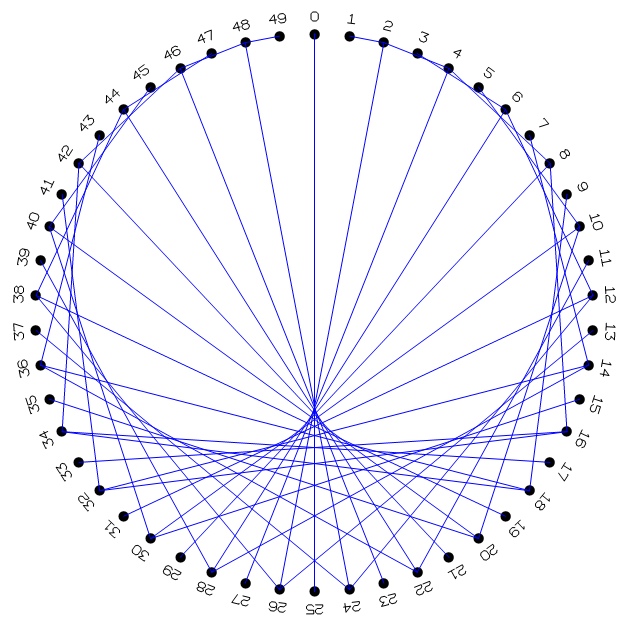
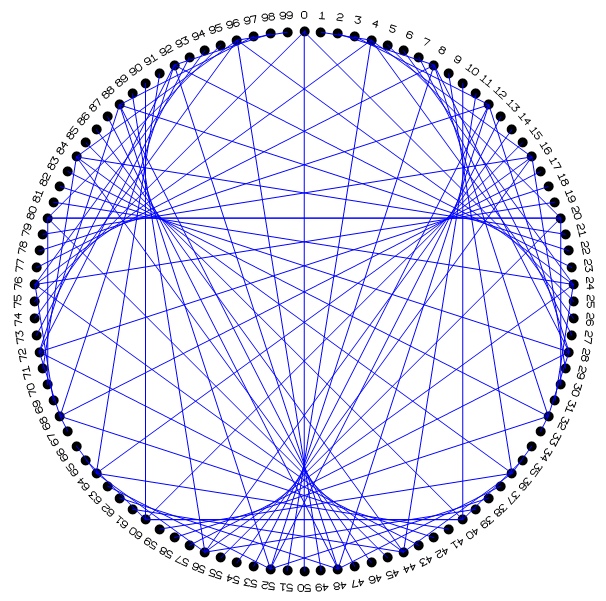
Part D. Optional Extension. The Cardioid

 

Ask students to consider using a larger ring, with 50 or more holes, and connecting each hole i to hole 2·i.   Hand out a sheet with 50 numbered dots and ask students to draw this on paper first.  They should discover that the strings outline (i.e., are tangent to) a curve called the "cardioid," because it is heart shaped, as shown above.  Note: A 30-dot sheet is not recommended. The shape does not stand out very clearly if there are fewer than 50 lines.

Ask students to plan how they might make the connecting hops on the back before starting construction.  Discuss ideas.  A modified version of the back-and-forth method works well here, going +1 on the back of the ring at the i end of each segment and +2 on the back at the 2i end of each segment.

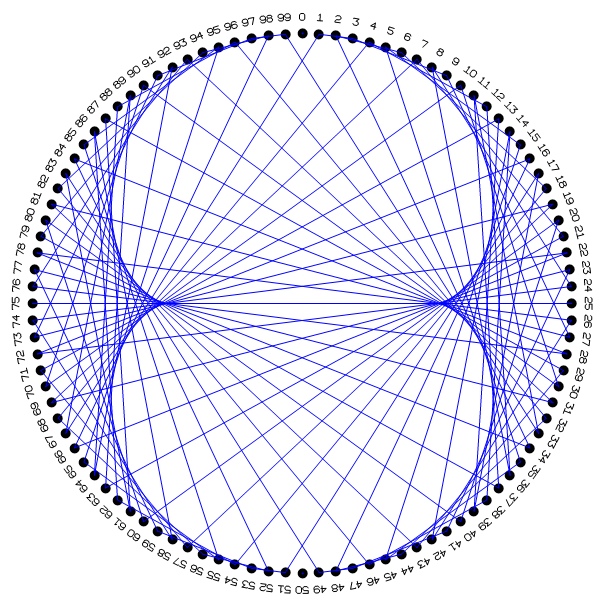
Hand out larger rings or show students how to create very large rings, as described below.  If making a 50-hole cardioid, have a length of string available equal to 40 times the diameter.  For a 100-hole cardioid, have 70 times the diameter.  Colored yarn works well with the larger rings.

For the modified back-and-forth method, start by attaching the string at 0, going on the back to 1, on the front to 2, on the back to 4, on the front to 2, on the back to 3, on the front to 6, on the back to 8, on the front to 4, on the back to 5, on the front to 10, on the back to 12, etc. 



Above is the state on a 100-hole extra-large ring after the i end has reached 25 and the 2i end has reached 50.

Above is the halfway point.  The 2i end has made a complete revolution while the i end has gone half way around. The completed cardioid is shown at the top of this page.

Optional Extensions

 

Beyond the cardioid. If you connect hole i to hole 3i you get the two-lobed pattern at left above, called a "nephroid."  If you connect i to 4i, you get the three-lobed pattern at right.  This one does not have a special name as far as I know, but it is "an epicycloid of three cusps" just as the nephroid is an epicycloid of two cusps and the cardioid is an epicycloid of one cusp.  These need a ring with more than 50 holes to be clearly visible.  Predict what happens if you choose some other k and connect each hole i to hole k·i.


Other Materials.  Find other materials to use as the ring, e.g., a hula hoop or an old bicycle rim.  Or bend a long thin strip of wood into a circle and mark locations to attach the strings.  You can run string between nails hammered into a wall or a board.

Larger Versions. Can you paint a mural-size version?   Or use sidewalk chalk in a parking lot.  How would you mark n equally spaced points on a very large circle?  How would you draw the long straight lines between points?


Detailed Instructions to Make Larger Rings

Time Required: 

Materials

Notes:
  1. The above activity with one-piece rings should be done first, so students understand the purpose of these larger rings.
  2. The arc is one tenth of a circle, but 20 pieces (two full circles) are required to make a ring, because of its double-layer construction.
  3. These templates are scaled to make a ring three feet in diameter with an efficient use of wood.  They can be scaled to arbitrary size.  To ensure rigidity, if you scale them to be larger, either use thicker plywood or extend the process below to use 30 arcs in three layers.
  4. Students can work in groups of two to four to make a ring, then string it as a group.

Steps

1. Distribute the parts to the groups. Ask students to lay out ten pieces in a neat circle on the floor, so they get a sense of its scale.

2. Ask students to lay out the second set of ten pieces on top of the first ten, so each piece in the top layer halfway overlaps two pieces in the bottom layer.  (For the 60-hole ring, each arc has 6 holes, so there should be a 3-hole overlap.  For the 100-hole ring, each arc has 10 holes, so there should be a 5-hole overlap.)


3. Hand out glue brushes and squirt some glue on to a scrap of cardboard or a similar palette for each group.

4. Instruct students to carefully brush glue on both surfaces that will join and to use just a small amount of glue---just enough to wet the surfaces.  Too much glue makes a mess, takes longer to dry, and doesn't make the joint any stronger.

5. Use the clamps to hold the two layers together.  Be sure the holes are well aligned, as the string will have to pass through both layers.  Wipe off any excess glue with a paper towel.


6. Allow undisturbed drying time for the glue to harden before removing the clamps.

7. The holes can be numbered with a pencil.  It is sufficient to just label the multiples of 5.

8. Use the rings as above to make large, impressive string figures.  Colored yarn works well.  Above is a three-quarters complete cardioid on a 3-foot diameter ring of 100 holes.
 

 9. You can see the back of the ring here, which makes clear how the back and forth method works.