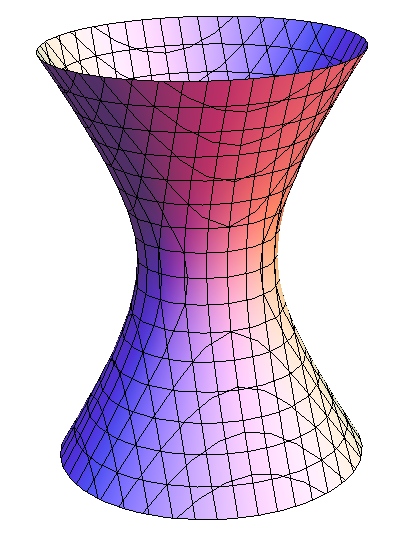
Hyperboloid

A hyperboloid is a mathematical surface with a surprising property. It is curved like an hourglass but can be made entirely out of straight lines. A hyperboloid can be understood by older students as a rotated hyperbola that has a simple quadratic formula. The form has important real-world architectural and engineering applications. In this workshop, students create a fun, flexible model of the hyperboloid from skewers and rubber bands, which will help them understand some of its mathematical properties.

This activity can be done by students of all levels if the mathematics is explained age-appropriately. It is an exciting way to make math visible in the classroom. Furthermore, it works as a team-building project, encouraging collaboration and mathematical communication. It is valuable for developing patterning skills and careful observation. In addition, it helps younger students develop fine motor skills.

The skewer hyperboloids are portable models for students to take home. After mastering the construction principles, the class as a whole can optionally make a single giant hyperboloid to leave on display in the school.

This activity provides rich classroom material for teachers following the Common Core Standards for Mathematical Practice. This lesson also offers cross-curricular connections to art, architecture, and higher-level strands of mathematics.

Detailed Instructions

Time Required: Up to 2 Hours

1 to 1.5 hours for individual hyperboloids
0.5 hour for optional large group hyperboloid

Materials

24 Shish kebab skewers per hyperboloid (12 inch long works best)
approximately 100 small rubber bands per hyperboloid (e.g., for pony tails or Rainbow Loom, http://www.amazon.com/Dream-Rubber-Bands-300s-Black/dp/B0014CCNJ4)

Optional Materials for Large Hyperboloid

24 or more bamboo sticks, dowels, or broomsticks (or in a large class, two per pair of students)
approximately 100 larger rubber bands

Notes

Chop sticks also work well, but are slightly shorter than the skewers so result in a smaller model.
If you are concerned about sharp tips on the skewers, you can choose to clip the tips off ahead of time with a saw.
Watch out for splinters from some brands of skewers.
This activity works best when students are in pairs. It can be adapted for students to work individually, but would require extra time.
The instructions are based on using 24 skewers and seven rows of rubber bands, but you could experiment with other numbers. Using more skewers will require more time. The number of rows of rubber bands should be approximately one third of the number of skewers. The photo at the top of this page shows 32 skewers and eleven rows of rubber bands.

Part A. In-Class Discussion

1. Introduce students to hyperboloids by showing images of the shape and pictures of large-scale applications such as observatories or cooling towers. Discuss the possible functionality of the shape. With older students familiar with the hyperbola, you can give an algebraic description as well.

2. Talk to students about the fact that mathematics is the study of patterns. Various branches of mathematics explore the patterns in different subject matter. The commonality is the desire for mathematicians to discover, understand, and extend patterns. Students at all levels are familiar with many kinds of patterns. For example, they are able to extend numerical patterns when we ask what is the next number in the series 3, 6, 9, 12, ... They are able to extend geometric patterns, rhythmic patterns, etc. Give students a few grade-appropriate examples as a minds-on puzzle activity. Here is an example of a fractal generation pattern:

3. Tell students that they will be creating a simple visual geometric pattern using lines, represented by skewers. Draw on the board to demonstrate the following pattern with two families of sticks. Point out that the ones slanting in one direction are always behind the ones slanting in the other direction. This seems like a simple idea, but we find it is counter-intuitive for many students who naturally want to weave the sticks with an over-under-over-under pattern or are not careful and make random crossings. Being able to visualize and reproduce this pattern is crucial for a successful hyperboloid construction.

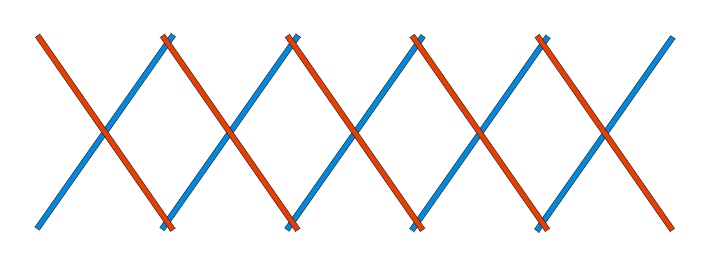
4. Ask students to draw the pattern using two different colors being careful to indicate how one family of sticks is always behind the other family of sticks. Ensure each stick crosses three other sticks, with one crossing at the midpoint and one near each end. Point out how the pattern can be seen as a series of overlapping X's.

Part B. Individual Constructions

1. Pair up students into teams of two. Hand out 24 skewers for each pair. Place small piles of rubber bands on each table.

2. Ask students to position some of their skewers to represent the pattern they have drawn. Students should check that one family of sticks is always behind the other family of sticks.

3. Show students how to take two skewers and wrap a rubber band around them three times. Slide the rubber band to the middle of the skewers and open the pair up to make an X. Demonstrate with a scissoring motion that you can switch from one way of slanting to the other way of slanting.

4. Ask a volunteer to come to the front of the class and make another X.

5. Ensure both X's look identical. Their slants must go the same way. Scissor one if necessary if they do not initially match.

6. Ask the volunteer to hold both X's beside each other with the ends overlapping as in their drawing. Point out that the tips might be in front or behind, but only one way gives the consistent pattern we are looking for. Wrap a rubber band (three times) around the top crossing. Wrap another around the bottom crossing. At this stage you should have a double X as in this image:

7. Tell students to work in pairs to make their own double X's. Check the crossing on each for consistency. Recommend that the rubber bands be placed an inch or more from the ends so they do not easily pop off.

8. Students may now extend the pattern to twelve X's using the twenty-four skewers. There should be three straight rows of rubber bands: one at the centers of the X's, one near the tops, and one near the bottoms. Ask students to double-check that the over-under pattern is consistent.

9. When a group has completed a row of twelve connected X's, double-check the over under pattern and use their model to demonstrate how to close it into a cylinder. An easy way to do this is for one team member to hold it upright on the table and curve it around while the other person places the two rubber bands that close the cycle. Ensure that those last two skewer crossings follow the consistent pattern. Ask all students to do the same, making a cycle of twelve X's.

10. Demonstrate how the top and bottom rows of rubber bands can be rolled towards the center row ("the equator"), making room for another row of rubber bands at the top and bottom of the cylinder. When you do this, new X's appear near the tips, inviting you to continue the pattern with an additional row of rubber bands near each end. At the end of this stage, there should be five straight rows of rubber bands.

11. Continue to roll the rubber bands towards the center so rows six and seven can be added. (Students have discovered that if the structure is worn like a hat by one partner, the other can add the rubber bands more easily.)

12. The structure is complete with seven rows of rubber bands. These rows should be adjusted to be straight and balanced for optimal aesthetic effect. By this point, students will discover how their hyperboloid can be flexed to create different shapes. If it is flattened down to a disk and let go quickly, it will pop up in the air.

13. Show this video to explain some of the mathematical ideas and suggest a larger construction.

Part C. Group Construction

1. As a fun culminating activity, the class can make a large hyperboloid out of broomsticks, dowels, bamboo, or any long sticks that may be affordably available. You might plan ahead to have one stick per person (rounded to an even number). This photo shows one made from twenty-four 48-inch dowels that can be purchased at a hardware store.

2. Begin by telling students how many sticks you have and asking them to think of a strategy for making a large-scale classroom hyperboloid. Two natural ideas that might emerge are (1) to lay the sticks on the floor making the flat X pattern as they did with the skewers; or (2) to have them stand in a circle and begin by making the cylindrical pattern of X's. Half the students can each hold two sticks in an X formation, while the other half of the students stand between them applying the rubber bands.

3. After the class agrees on a strategy, let them take over and build. Let students decide how many rows of rubber bands make for the best hyperboloid.

Further Explorations

Variations. What happens if you change the number of sticks from 24 to something else? What happens if you change the number of rows of rubber bands from 7 to something else?

Applications. Explore applications of the hyperboloid in cooling towers, observation towers, art, architecture, gears, etc.

Formulas. You can explore hyperboloids algebraically by plotting the equation a x^2 + b y^2 - c z^2 = d^2 with 3D graphing software.

Combining Models. You can stack skewer hyperboloids into a giant tower. In what other ways can you combine them?

Spacings of the Crossings. The spacing of the points along any one stick where it crosses the sticks in the other direction is not constant. The crossing points are closer together near the "waist" of the hyperboloid and further apart as one moves towards the ends of the sticks. With trigonometry, students can determine the exact spacings. Begin with a 2D projection onto the XY plane.