Making Math Visible

Paper Triangle Ball



The Paper Triangle Ball is part of a family of "slide-together" paper constructions that are made by cutting a number of identical pieces of paper which fit together without tape or glue.  In this two-part workshop, students first make a solid-color model to understand the mechanics of the structure.  Then color is introduced for the second part in which twenty triangles of five different colors are assembled.  This is a logic puzzle that is a great exercise in problem solving.  Students get to use spatial reasoning to discover and extend geometric and coloring patterns.  When complete, students will have created a colorful orb which they can take home or use to decorate the classroom.  There is also a nice visual surprise in which students will see a cube hidden in the edges of the resulting construction.

The Paper Triangle Ball is a wonderful activity for middle and high school students to develop concrete and mental visualization. It can be done with younger students if they have had previous experience with paper constructions.  This activity works as a team-building project, encouraging collaboration and mathematical communication.

This a great example of modular kirigami (assembling cut pieces of paper) and a good preparation before more complex paper constructions.  In general, explorations with paper can be mathematically rich, inexpensive, and accessible ways for students to start thinking three dimensionally.

Before attempting this construction, students should have built all five Platonic solids, to be familiar with their geometry and making 3D objects from paper.

This activity provides rich classroom material for teachers following the Common Core Standards for Mathematical Practice.  This lesson also provides cross-curricular connections to art, architecture, and higher-level strands of mathematics.

Detailed Instructions

Time Required:  1.5 to 2 Hours

Materials

Notes
  1. Copy the template onto the card stock ahead of time.  Only card stock will work.  Ordinary copy paper is too thin.  Card stock is a heavy weight paper, stiffer than standard paper, but thin enough to snake through the rollers of a copy machine or laser printer. Most copy shops have a selection of colors on hand that they can copy on to for you, or you can buy it by the ream to put in your own copier.
  2. Each Paper Triangle Ball is made of twenty triangles.  There are eight triangles on the template sheet, so two and a half sheets are required to make one orb.
  3. The activity works best when students work in pairs or at most in groups of three.  It can be adapted for students to work individually, but would require extra time.

Steps

Part A --- Solid Colored Ball
1. Group students into pairs.  Hand out scissors and the printed White card stock sheets.  Each pair of students needs two and a half sheets. 
 
2. Tell students to cut out twenty triangles and individually cut the three slots in each.  Neatness counts!  Warn students NOT to stack the sheets or the triangles, trying to save time and cut through several sheets at once; that would be too inaccurate.

3. After most groups have cut out at least ten triangles, tell students that we will begin exploring the shape now and that they can finish cutting later.  Pose the following puzzle, adding these hints gradually, giving students time at each stage:
Encourage students to hold up and share their discoveries and give more hints as needed.  Students will likely discover a tetrahedral structure with four 3-sided holes, an octahedral structure with six 4-sided holes, and various irregular and planar structures.  Discuss the properties of these structures, encouraging students to keep exploring. Eventually a group will find the configuration with twelve pentagonal holes, as pictured above.

Inform students that is it easier to add one triangle at a time rather than trying to join larger sub-modules.  Suggest they use teamwork, with one partner holding the partial orb in the air while the other attaches additional triangles.  Laying it flat on the table will cause it to lose its shape.

Groups of students who have completed their orb can then help other teams.
 


4. Ask students to examine the final result and to determine how many pentagonal holes it has.  Encourage students to think systematically instead of counting holes individually.

5. Challenge students to find a cube hidden in the structure.  They will need to look at the edges of the triangles as separate line segments.  First have them search for a group of four segments that make a square.  The square can then be extended to a full cube. 



Part B --- Multi-colored Ball

6. Hand out the printed color card stock sheets.  Each pair of students needs a half sheet in each of the five colors.  They will have a total of twenty triangles: four in each of five colors.

7. Instruct students to cut out the triangles and make the same structure but with a coloring rule: Each of the five colors should appear around each hole.  The colors can be in any order but can not be repeated around any one pentagonal hole.  For example, no hole should have two red triangles around it.

8. Walk around the room checking how the constructions progress, helping students and pointing out any problems as early as possible.  A common problem is not sliding the slots completely into each other.  Be sure always to keep the corners of the triangles on the outside of the construction, so the boundary of each triangle is completely visible. Double check as you go along that every pentagonal opening is surrounded by five different colors. Keeping the triangles flat (planar) and having the corners meet crisply is the key to producing a neat geometric impression.

Warn students that the problem is harder than it looks and they will have to think logically.  Sometimes they may need to partially undo some of their construction to try a new color pattern.  Some students may need more coaching and guidance than others.  For example, pointing out to think ahead of time which colors can be ruled out for a given position because it would create a color conflict in a neighboring pentagon.

Eventually some students will complete their Ball in a consistent way and will be able to help their neighbors.

9. When complete, ask students to examine their Paper Triangle Ball more closely to see a cube as before.  You can ask how many there are and see if they can find that there are five cubes.  Each cube has twelve edges, so the five cubes use a total of sixty edges, which come from the twenty 3-edged triangles.

10. You can conclude by showing this video illustrating a family of related paper constructions that might inspire students to explore further.

Extensions

11. Ask students to examine the color pattern on each other's Paper Triangle Balls to determine whether all the balls in the room are identical.  Are there many different color patterns?  They should find that sometimes they can take two balls and rotate one so it exactly matches the other in all twenty triangles.  In other cases, the two balls are distinct solutions. In total, there are four possible legal solutions for coloring the whole ball.

12. The idea can be applied at a larger scale. Large cardboard versions about five feet in diameter can be made from sheets of cardboard.

13. You can ask students to find a rule that anyone could use to select the appropriate color as they put the structure together.  After starting with five triangles to make one pentagonal hole, the rule should look at what is already made to tell you what color you should place in a desired location. 



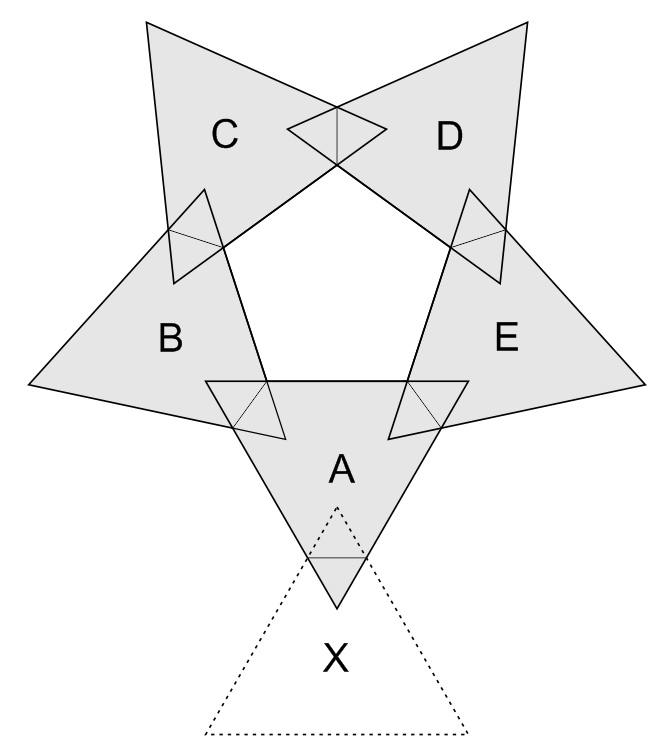
Here is a rule that works, which some students might discover after studying their completed orb.  If ABCDE is a pentagon of triangles already assembled, when connecting a new triangle into A, in the position X, choose the color of X to be the color you observe at position C.  You must do this throughout the entire structure.  An alternative rule is to use the color from D as long as you do that throughout the entire structure.

14. For older students, you can discuss the combinatorics of the colors surrounding any triangle.  Given any triangle, there are three neighboring triangles that it slots together with. Given five colors, ABCDE, how many ways can you choose a subset of three?  Answer: ten. ABC, ABD, ABE, ACD, ACE, ADE, BCD, BCE, BDE, CDE.  Students can be led to observe that each of those ten combinations happens exactly twice on their Ball.  The two positions will be exactly opposite and in reverse order, e.g., if one triangle is surrounded by colors ABC in clockwise order, then the opposite triangle will be surrounded by ABC in counterclockwise order.

15. The combinatorics of the colors surrounding the twelve pentagonal openings involves the "even permutations" as discussed in the Extensions for the Paper Square Ball activity.

References

Charles Butler first described this design to us.

Portions of this material appeared in the 2004 Bridges Conference booklet of Teacher Workshop materials.